Addition avec le complément à deux

Considérons d'abord le cas d'une addition sans débordement (on ne considère que les n bits résultats d'une opération sur deux nombres sur n bits). Détaillons les 4 cas (selon les signes des opérandes) :

5	00101	-5	11011	-5	11011	5	00101
9	01001	-9	10111	9	01001	-9	10111
14	01110	-14	10010	4	00100	-4	11100

Comment est-ce possible ? Cas de l'addition de X et Y deux entiers négatifs. Soit Z = X + Y. En complément à deux, $- \ensuremath{\mid X \mid} = 2^n - \ensuremath{\mid X \mid}$. Donc

$$\begin{eqnarray*}Z &= & (2^n - \ensuremath{\mid X \mid} ) + (2^n - \ensuremath{\... ...uremath{\mid Y \mid} )\\ &= & 2^{n+1} - \ensuremath{\mid Z \mid}\end{eqnarray*}$$

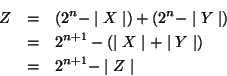
ce qui sur n bits donne bien 2ⁿ - .

Considérons le cas du débordement : il y a débordement si

• les opérandes X et Y sont de même signe, et
• + $\geq 2^{n+1}$

	13	01101	-13	10011
	9	01001	-9	10111
sur n bits	-10	10110	10	01010
sur n+1 bits	22	010110	-22	101010

Le débordement peut être détecté :

• en comparant le signe des opérandes au signe du résultat : s'ils sont différents, il y a débordement, ou
• en comparant la retenue entrante dans le bit de poids fort avec la retenue sortante : s'ils sont différents, il y a débordement.

? Comment fonctionne l'addition de nombres codés en complément à 1 ?