Multiplieur à base plus élevée (radix-4 modified Booth recoding)

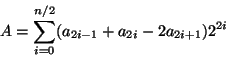
Une multiplication à base plus élevée (sous entendu que 2) considére plusieurs bits simultanément (au lieu de 1 habituellement). Ainsi, un multiplieur à base 2^k considère k bits simultanément.

! Le nombre de produits partiels est divisé par k.

Considérons un multiplieur à base 4. On considère les bits deux par deux, en s'appuyant sur le bit précédent la paire courante. De plus, on emploi un recodage de Booth. Pour un nombre A, on a

$$A = \sum^{n/2}_{i=0} (a_{2i-1} + a_{2i} - 2 a_{2i+1})2^{2i}$$

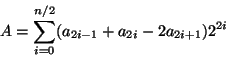
avec a_-1=0 (par exemple, 3 = $2\times 2^1 -1 \times 2^0$)

! Une multiplication par la base = un décalage vers la gauche.

L'opération à faire sur le résultat intermédiaire est donnée par la table suivante (en fonction des bits du multiplicande A) :

a2i+1	a2i	a2i-1	résultat intermédiaire
0	0	0	0
0	0	1	+B
0	1	0	+B
0	1	1	+2B
1	0	0	-2B
1	0	1	-B
1	1	0	-B
1	1	1	0

Exemple : la multiplication de 7 (A = 00111) par 3 (B=00011) se fait comme suit :

					0	0	1	1	1
				$\times$	0	0	0	1	1
				-	0	0	0	1	1	(-B)
	+	0	0	0	1	1				(+2B)
0	0	0	0	0	1	0	1	0	1

? Donner la table permettant de déterminer le multiplicande intermédiaire à ajouter pour une multiplication en base 8.